Searching for alternatives to material implication

This journey of my research has begun when we learnt about material implication in the University of Szeged. There was an exercise in the Discrete Mathematics book that we were solving on a lesson, and I did not agree with the official solution. I am probably not allowed to copy the example here, but I can share a sentence with a similar structure:

- Suppose that Andrew says that his hat is red only if Adam's hat is green. But Adam says that if his own hat is not green, then Andrew's hat is red. Can both of them be right?

If we use the truth table of material implication for conditional statements, and we use the same thing for "only if" constructs, then it's possible that both of them say the truth. My natural brain, however, felt that it is too strange. That's why I spent some time thinking on this occasionally, with mixed results. During my research, I have come across another strange example:

- Suppose that Andrew knows that there is no electricity supply, and he also knows that if there is no electricity, the lights cannot shine. Adam, however, knows that the switch is off. Is the following sentence true or false: "If the switch is on, the lights shine"?

According to the truth table of material implication Adam immediately knows that the sentence is true, for "everything comes from a false statement". This means that the sentence should be true according to Andrew's knowledge as well. According to the truth table of material implication this is OK, because we can suppose that the switch is never on. Yet here we can also feel something strange.

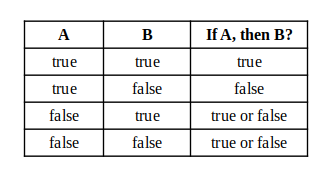
Many Logicians and Mathematicans have also had strange feelings about material implication. That's why some of them defined other kinds of implication, like indicative conditional, strict conditional, entailment, or even theories like relevant logic, and some others have written publications about the issue, like William Kneale and Martha Kneale wrote The Development of Logic. There's an entire chapter in it about the implication relation, about the ancient disputes of Philo the Dialectician, supporter of material implication against Diodorus Cronus, supporter of a stricter definition. The Development of Logic concluded that the truth table of a better implication should not fix the truth value of the implication in case the first sub-statement is false, like on the pictures. I share two pictures instead of one because I don't remember exactly what was in the book, but these two pictures are equivalent.

There was a time when I did not stop here. I had the following suppositions:

- Every true statements come from a true statement.

- Every true statements come from a false statement.

- A true statement comes from everything.

- A false statement does not necessarily come from another false statement.

Based on these premises, I could improve the truth table in a following way:

For some time, I believed that I've discovered the real implication here. There was another reason of thinking this: this way I could exclude the equivalence of A=1 and A=2 if A=3 and other things are unknown. Then I promoted this on a forum about philosophy, and people have attacked it, of course. They did not manage to disprove my arguments, but they have stimulated my thoughts in a way that enabled me to believe that I can disprove my arguments myself. In the antiquity, people did not use truth tables, but they used syllogism!

It was challenging to try to exclude the case of (false, false, false) in the truth table of implication, and in fact, this is possible by syllogisms...

1. Modus Tollens is true always:

If (If B Then A) and (Not A) Then (Not B)

2. The following is the only one assumption:
If B Then A

3. If the assumption and Modus Tollens are true, then this is true:
If True and (Not A) Then (Not B)

4. So if the assumption is true, then this is true:
If (Not A) Then (Not B)

5. Thus the following is always true:
If (If B Then A) Then (If (Not A) Then (Not B)).

6. Thus the rule of contraposition is correct.

7. If C is false and D is false, (Not C) is true and (Not D) is true, and "If (Not C) then (Not D)" is true.

8. From the previous assumptions in (7), the rule of contraposition says that "If (Not (Not D)) then (Not (Not C))" is true, in other words, "If D then C" is true.

9. This also means that if A is false and B is false, then "If A Then B" is true.

Thus we can use the rule of contraposition to exclude the other extra row from the truth table as well, so we get the truth table of material implication we learn about in schools!

At least they could provide a proof like this to it when we learn about it... but wait... the strange feelings about the material implication are still not resolved! How to resolve them? This is your homework! (Just kidding.) More seriously, I really feel that these strange feelings can be justified one day, when the knowledge of humankind advances... maybe I'll publish something else about in this blog (or elsewhere) later.

Currently, I conjecture that the solution would be about undetermined truth values of statements, which is against the materialistic worldview, but still a possibility. This means, for example, that something in the future can be either true or false, so not predestined. At least, it seems that these strange feelings of our soul come from an unconscious faith in this freedom, which has implications on our view of logical statements.